Goals: the NFL’s
There are systems that we have to make sure that we maintain (parity).
Carefully constructed system of competitive balance that makes NFL games and championship races so unpredictable and exciting.
Roger Goodell, NFL commisioner
If you expect something to happen in this league, it’s likely not going to happen.
Jonathan Kraft, President of New England Patriots
Goals: ours
- Develop model to assess parity in professional sports
- Does the NFL have parity?
- How do NFL systems impact league outcomes?
Assess parity in professional sports
How to define parity
the state or condition of being equal
Google
Assess parity in professional sports
What parity looks like:

Assess parity in professional sports
What parity does not look like:

A cross-sport model to assess parity
- \(p_{(q,s,k)ij}\) is probability that team \(i\) will beat team \(j\) in season \(s\) during week \(k\) of sports league \(q\), for \(q \in \{MLB, NBA, NFL, NHL\}\).
- \(\alpha_{q_{0}}\) be the league-wide home advantage (HA) in \(q\)
- \(\alpha_{(q) i^{\star}}\) be the extra effect (+ or -) for team \(i\) when playing at home
- \(\theta_{(q,s,k) i}\) and \(\theta_{(q, s, k) j}\) be season-week team strength parameters
A cross-sport model to assess parity
\[ E[\text{logit}(p_{(q,s,k) ij})] = \theta_{(q,s,k) i} - \theta_{(q, s, k) j} + \alpha_{q_0} + \alpha_{(q) i^{\star}} \]
Assumptions:
- \(\sum_{i=1}^{t_{q}} \theta_{(q,s,k)i} = 0\)
- \(E[\theta_{(i,q,s+1,1)}] = \gamma_{q, season} \theta_{(i, q,s,k)}\)
- \(E[\theta_{(i,q,s,k+1)}] = \gamma_{q, week} \theta_{(i, q,s,k)}\)
- \(\gamma_{q,week}\) and \(\gamma_{q,season}\) week/season level autogressive parameters
A cross-sport model to assess parity
What can our model tell us? A parity checklist
- Unpredictability at a fixed time (variability of \(\theta_{(q,s,k) i}\)’s)
- Within season unpredictability (\(\gamma_{q, week}\))
- Between season unpredictability (\(\gamma_{q, season}\))
A cross-sport model to assess parity
Data: 2006-2016 regular season games in MLB, NBA, NFL, NHL via Sports Insights
Priors: Uniform (variance parameters) and Normal (team strength parameters)
Software: rjags package in R statistical software
Draws: 20k iterations, 2k burn in, thin of 5
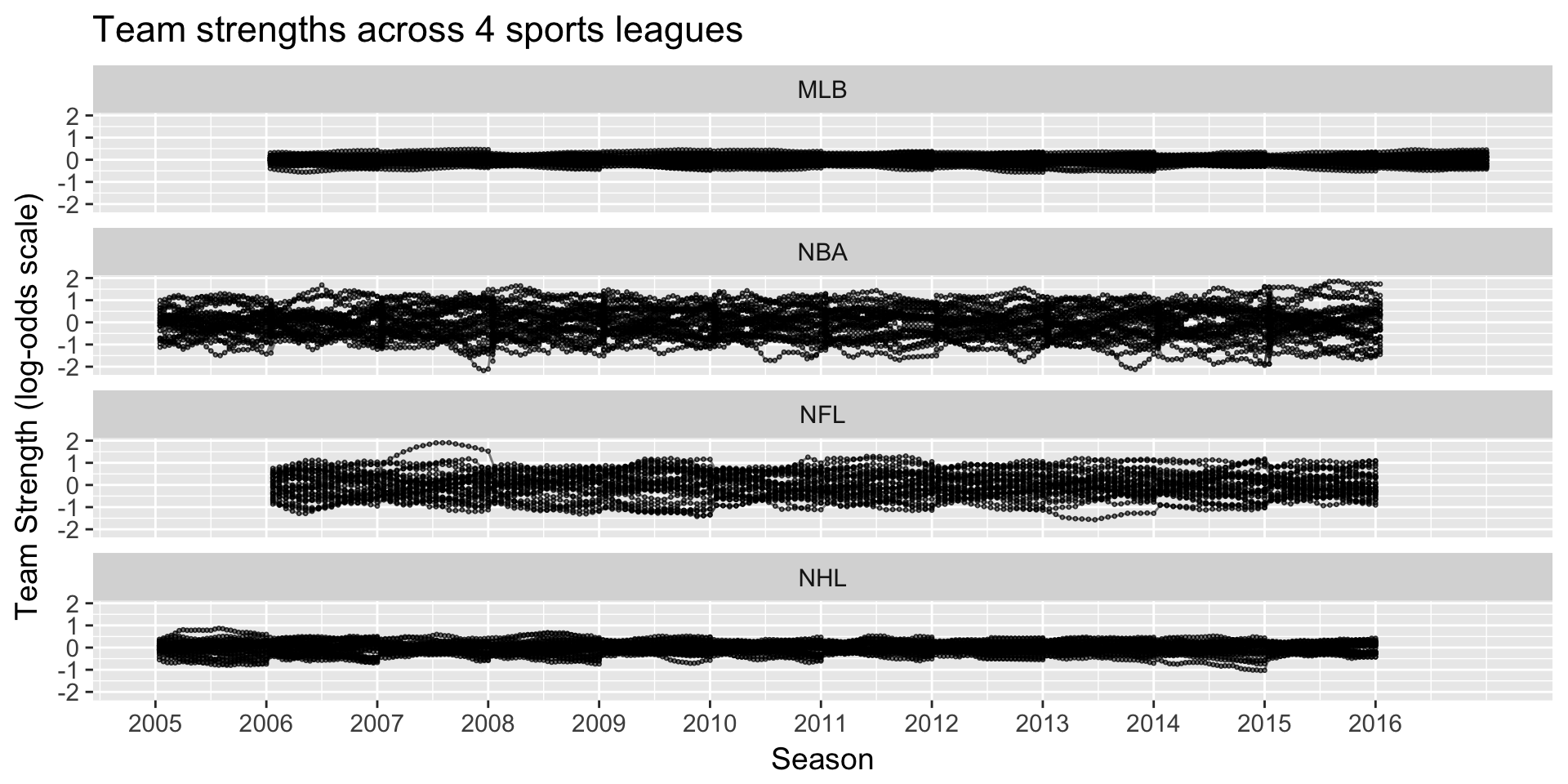
Model estimates
Model estimates
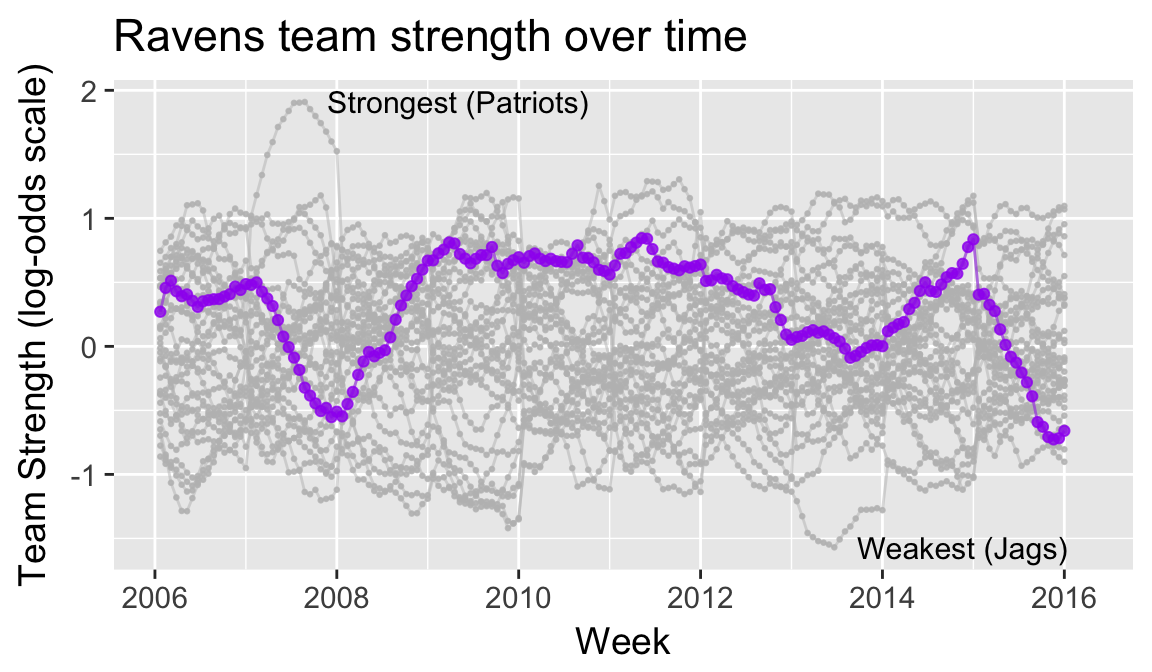
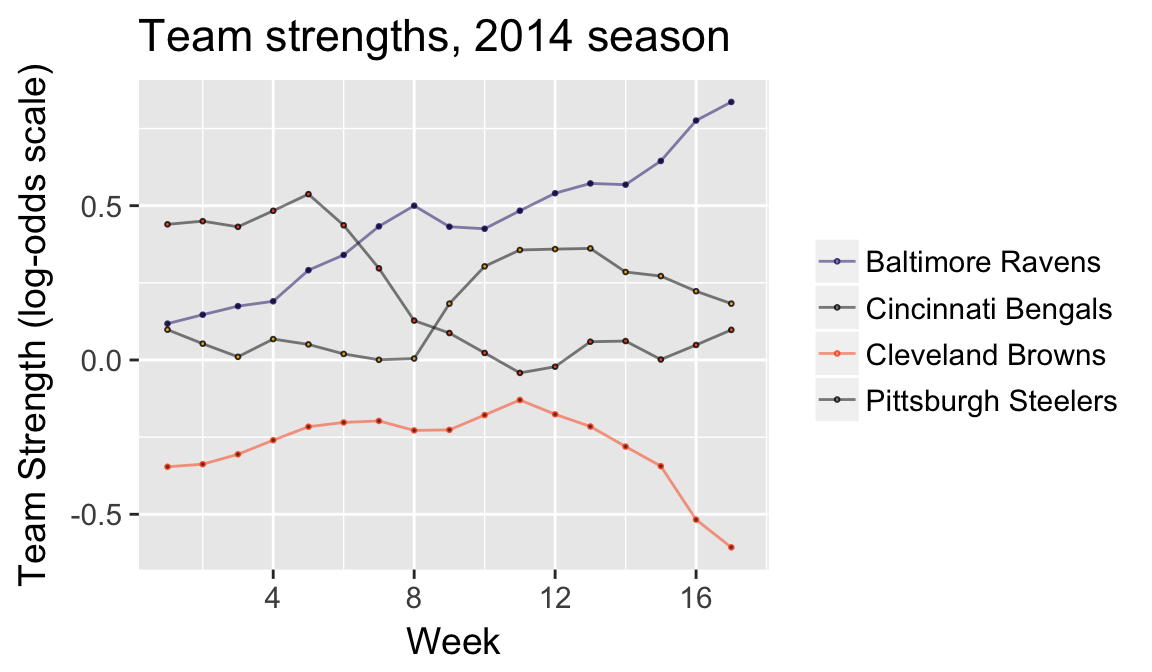
NFL’s parity: unpredictability at a fixed point in time
How often does the best team win?
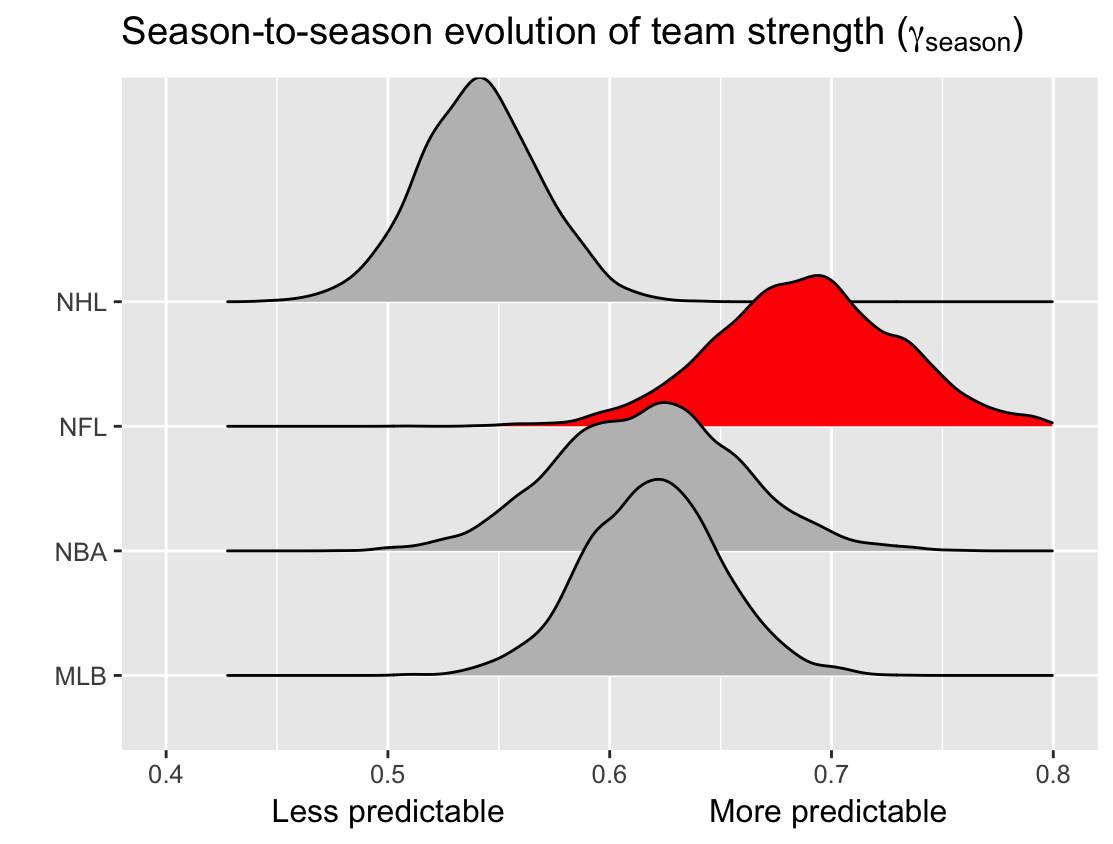
NFL’s parity: unpredictability by season
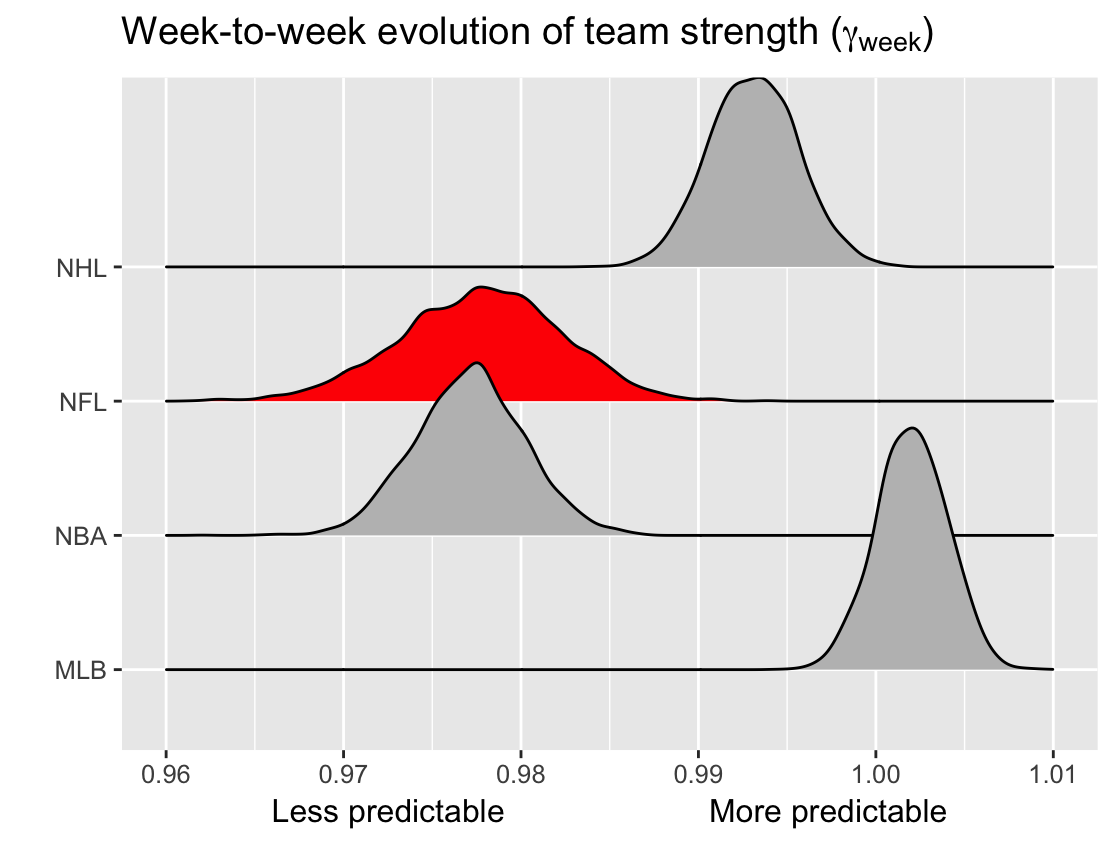
NFL’s parity: unpredictability by week
NFL systems that impact perceived parity
- Small number of games
- Single elimination tournament
- Unbalanced schedule (focus of today)
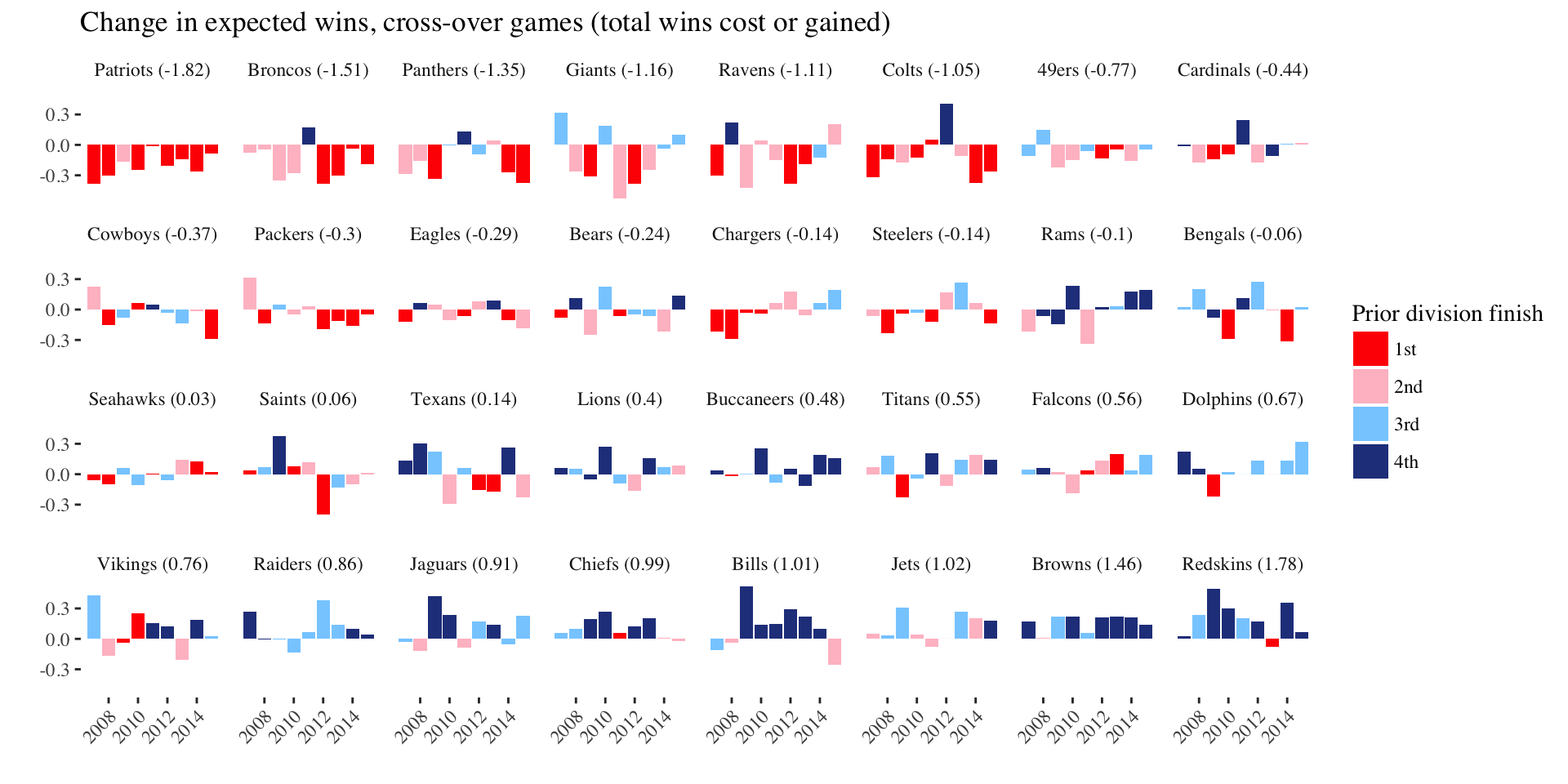
Effect of NFLs unbalanced schedule
2 games per year against like-placed teams from prior year (I’ll call them “crossover” games).
\(Hypothetical\): What if league-average teams were played instead?
\(Approach\): Use team strength estimates to approximate change in expected wins
Effect of NFLs unbalanced schedule
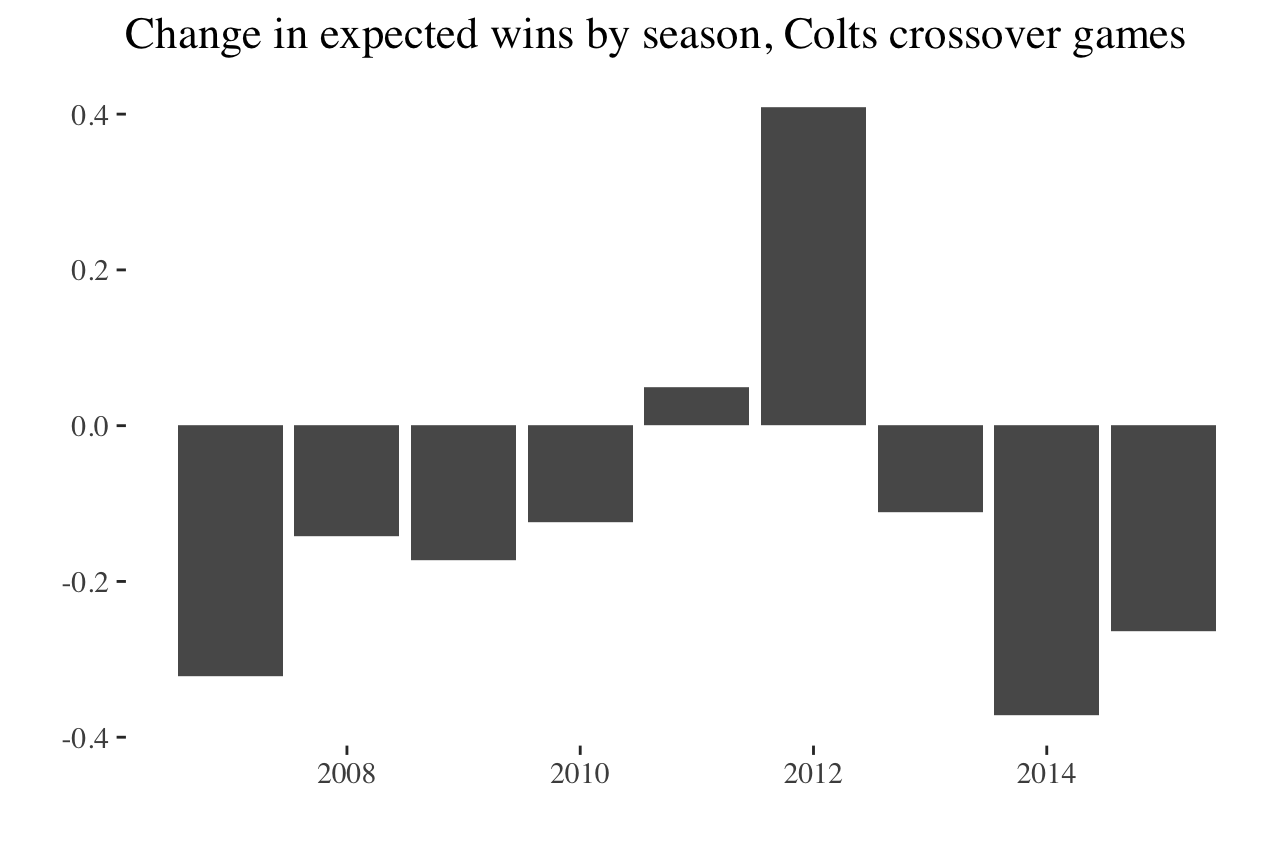
Effect of NFLs unbalanced schedule
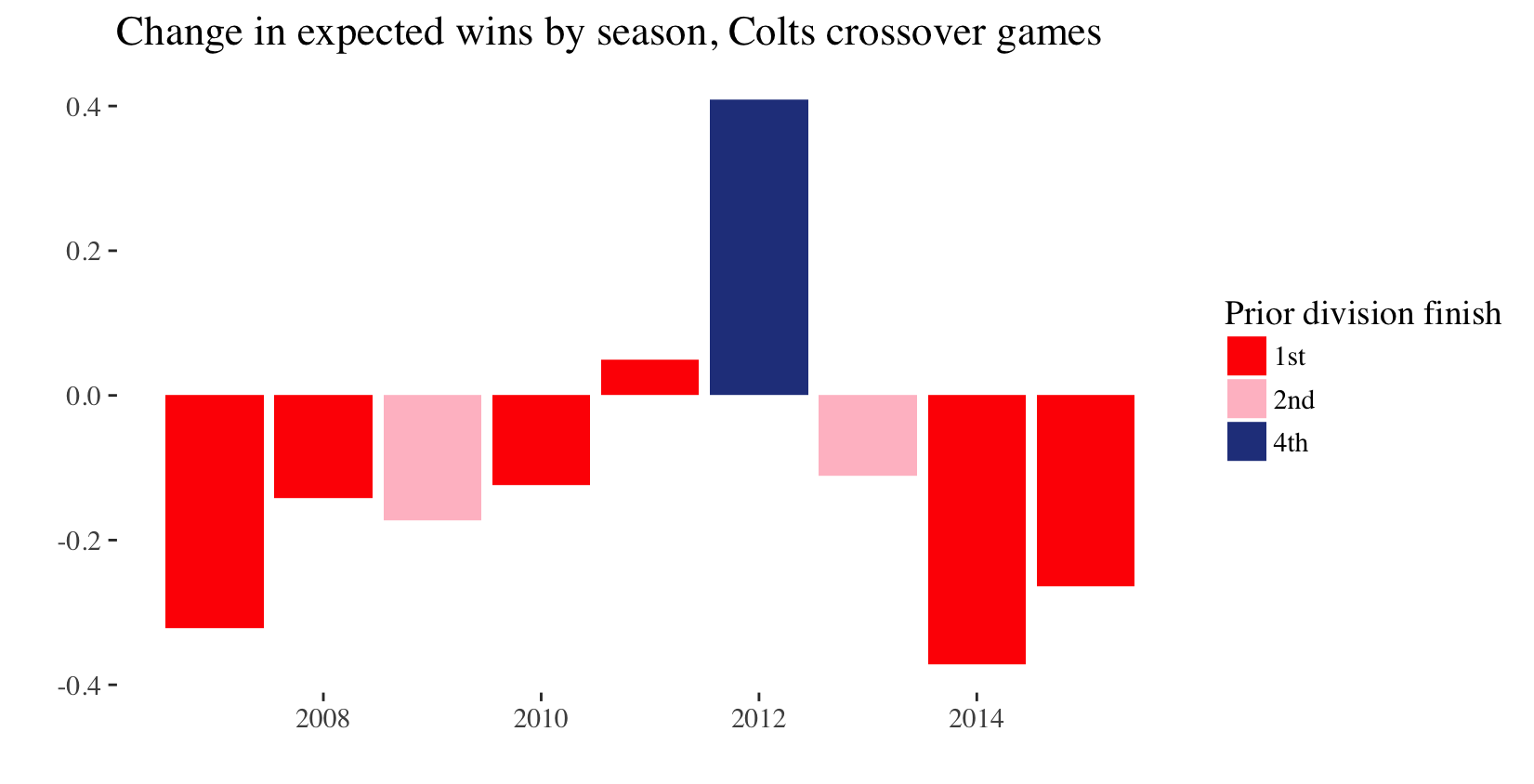
Effect of NFLs unbalanced schedule
- Difference between last and first place in a division worth approximately one-third of a win in year following
- Practical significance given 16 game schedule
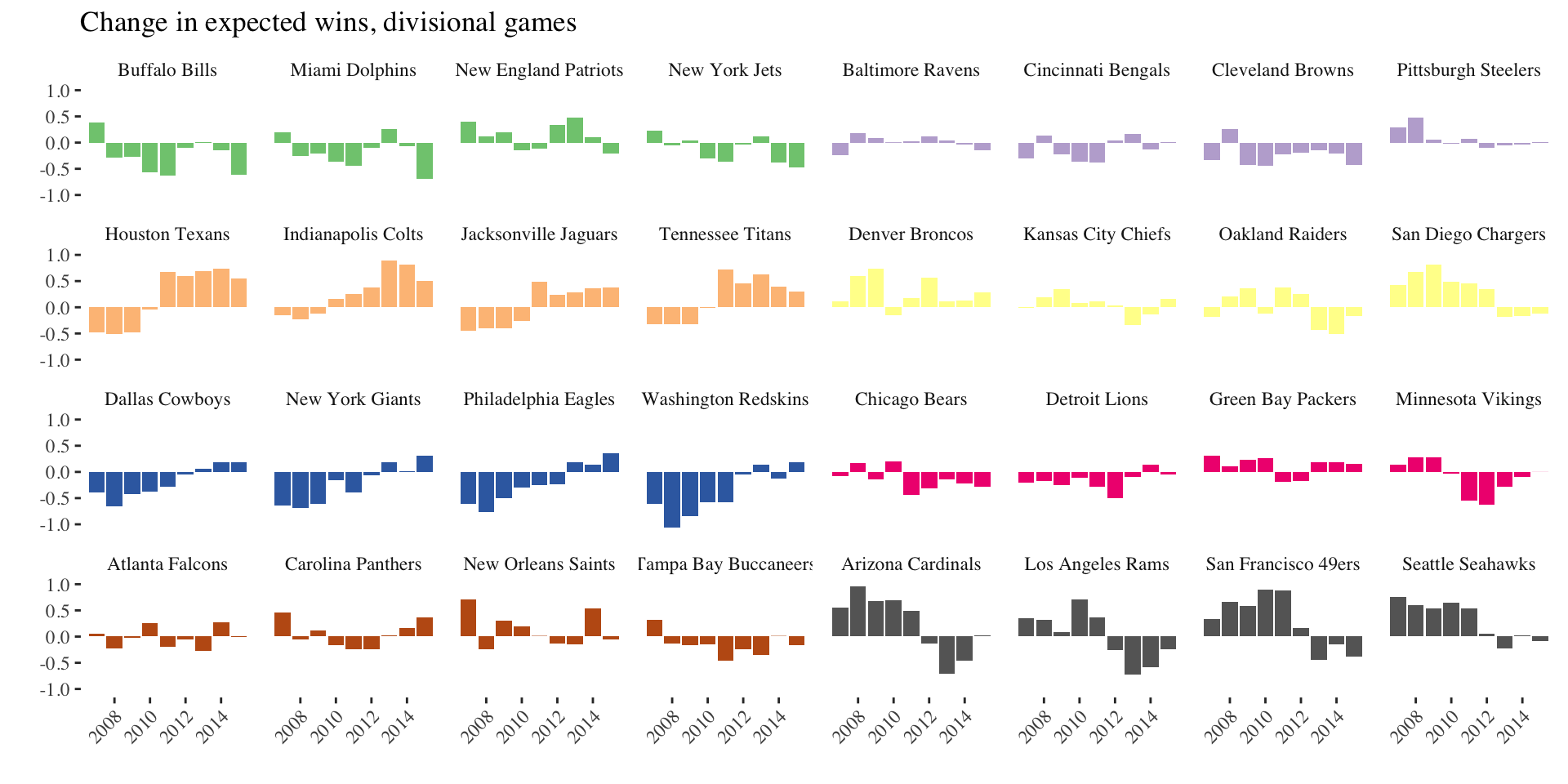
- Alternative effects: divisional games
- Future work: compare to other sports
Conclusion
Does NFL have parity? Not particularly
Conclusion
Do NFL systems push records to 0.500? Sort of
Acknowledgements: Greg and Ben


Summary: parity in the NFL
- Unpredictability at a fixed time ❌
- Within season unpredictability ✔️
- Between season unpredictability ❌
- Crossover games drive records to 0.500 ✔️
More info: Paper (link) & Github (link)