Bayesian additive regression trees for causal inference with multiple treatments

3 lung cancer treatments

Video assisted (VATS)

3 lung cancer treatments

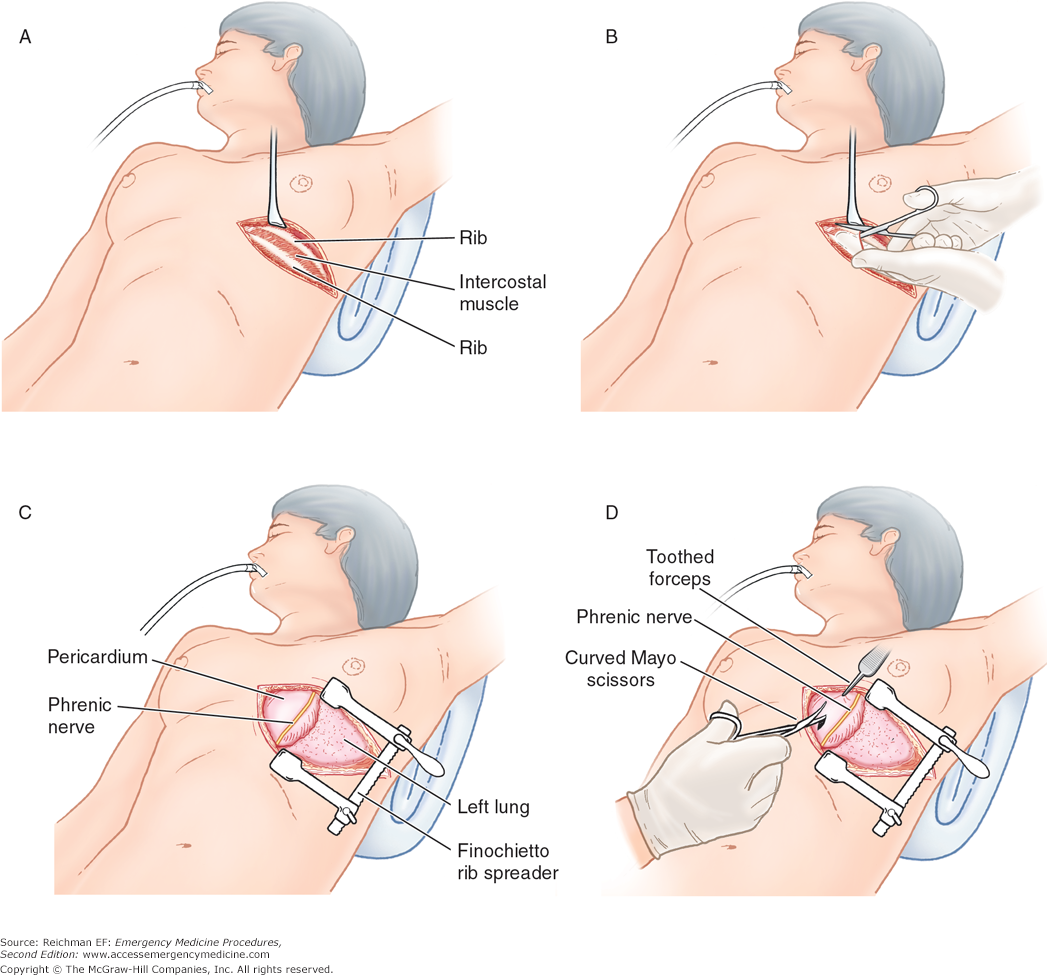
Open thorectomy

3 lung cancer treatments

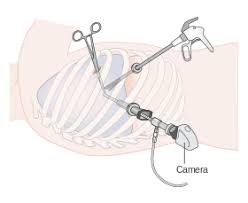
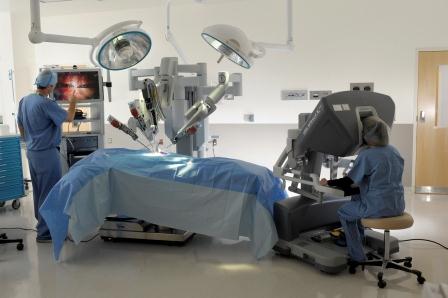
Robotic assisted

3 lung cancer treatments

3 lung cancer treatments

3 lung cancer treatments

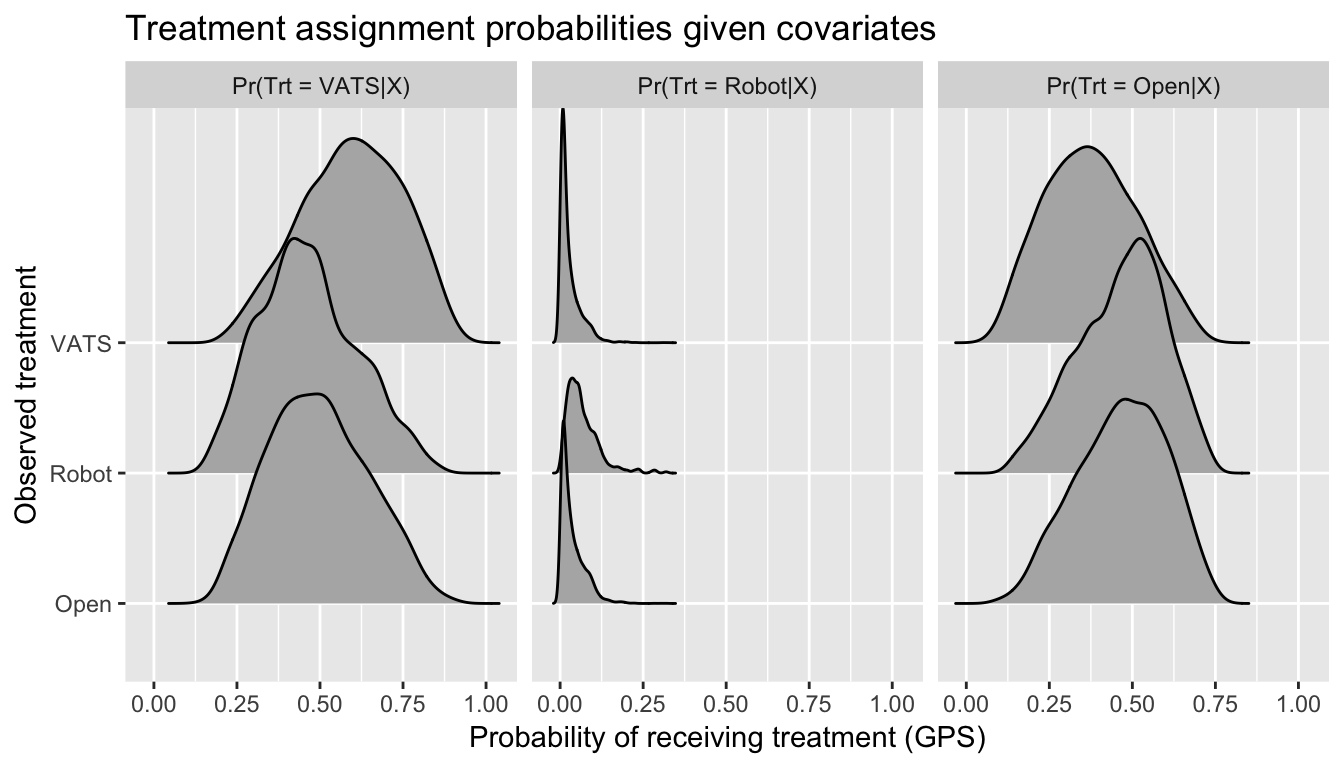
Issue 1: Selection bias

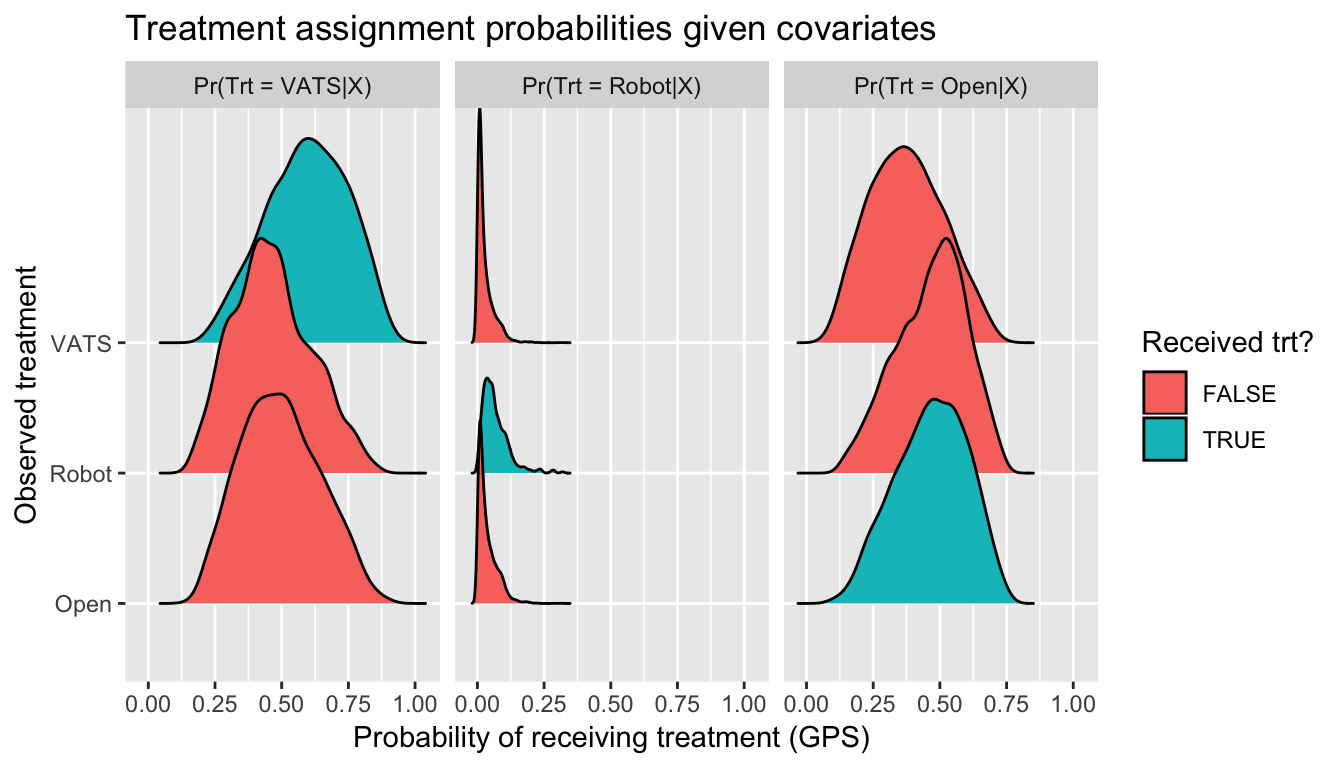
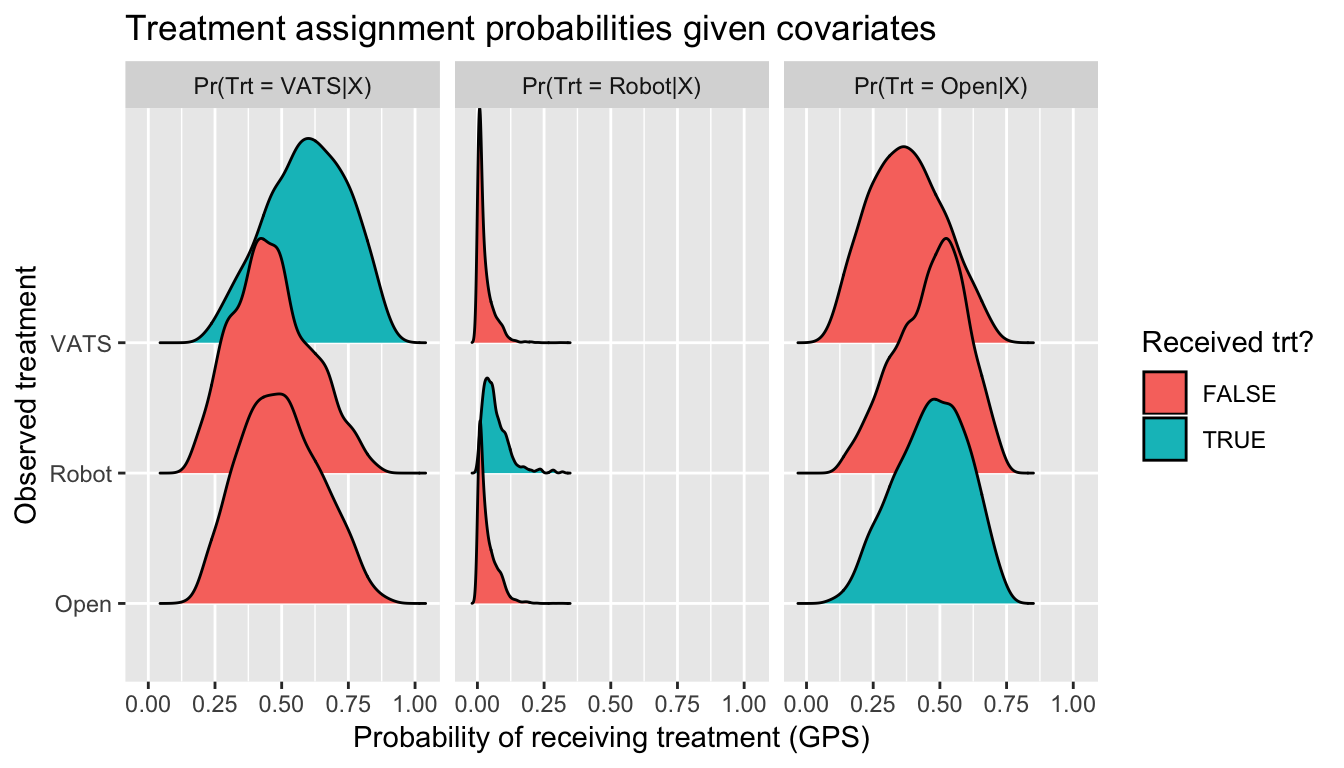
Issue 2: Non-overlapping distributions

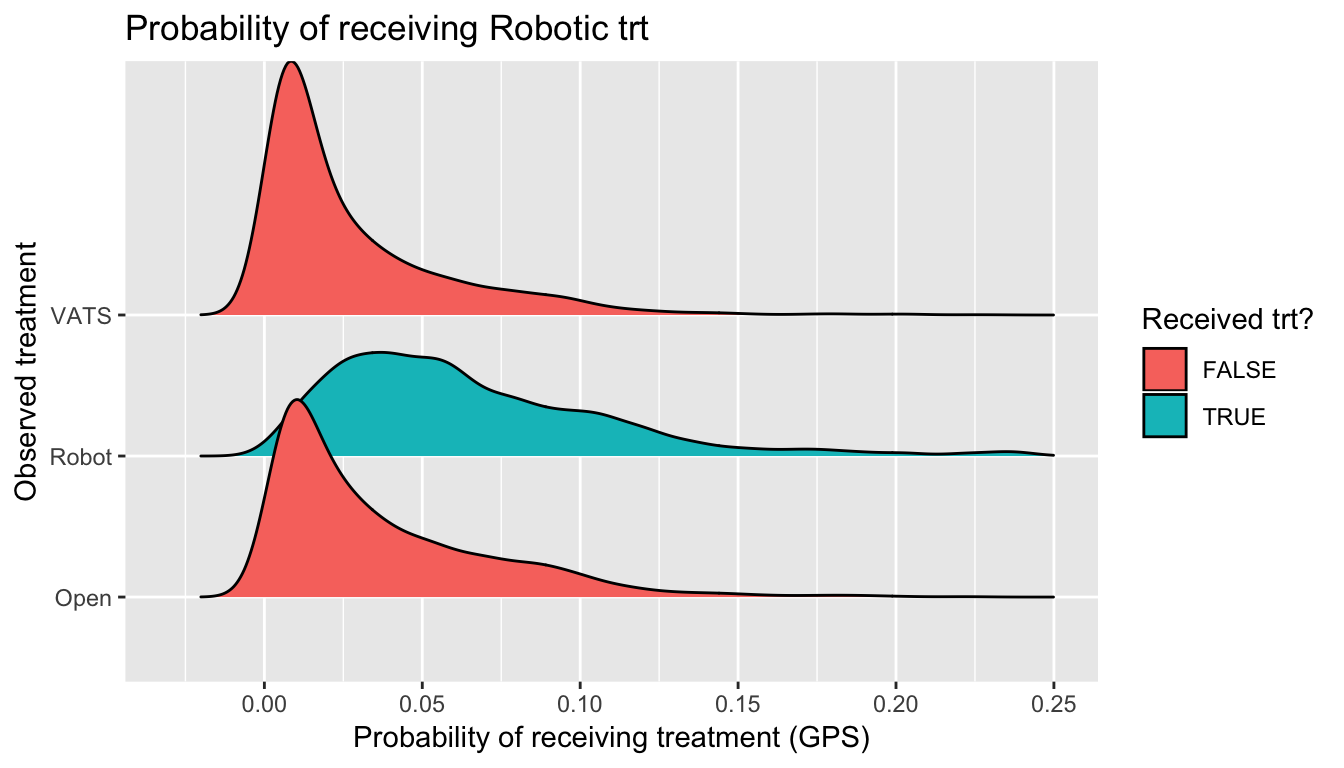
Issue 3: Large weights

Notation

Consider causal effect of $A \in \{1, \ldots, Z\}$ on binary outcome $Y \in \{0,1\}$

• $i = 1, \ldots, n$ for $n$ total subjects
  • $n = n_1 + \ldots + n_Z$
• $\{Y_i(1), \ldots, Y_i(Z)\}$ as potential outcomes for $i$
• Covariates $X_i$

Notation

Interest: average treatment effect among treated

• $ATT_{1|1, a}$: effect of $T = 1$ versus $T = a$ among those with $T = 1$
  • $ATT_{1|1, a}$ = $\frac{1}{n_1} \sum_{i:A_i = 1} (Y_i(1) - Y_i(a))$ for $a = \{2, \ldots, Z\}$

• Ex: $Z$ = 3, $ATT_{1| 1, 2}$, $ATT_{1| 1, 3}$, $ATT_{1| 2, 3}$
  • $ATT_{1|1, 2}$ = $\frac{1}{n_1} \sum_{i:A_i = 1} (Y_i(1) - Y_i(2))$
  • $ATT_{1|1, 3}$ = $\frac{1}{n_1} \sum_{i:A_i = 1} (Y_i(1) - Y_i(3))$
  • $ATT_{1|2, 3}$ = $\frac{1}{n_1} \sum_{i:A_i = 1} (Y_i(2) - Y_i(3))$

Causal inference with multiple treatments

Why not binary approaches?

• May not fully account for differences in patient characteristics
• Comparisons of disctinct cohorts with dissimilar characteristics
• Challenging to identify optimal treatment
• Main issue: matching on scalar alone insufficient
• See Lopez & Gutman, 2017 for more

Causal inference with multiple treatments

• Inverse probability of treatment weighting (Feng et al, 2012)
• Generalized boosted models (McCaffrey et al, 2013)
• Matching (Yang et al, 2016; Lopez & Gutman, 2017)

Bayesian Additive Regression Trees

Why BART for causal inference? see Hill, 2012

• Flexibly models response surface ✔️
• Large number of continuous and categorical predictors ✔️
• No ambiguity with respect to balance assessment ✔️
• Accessibility ✔️
• Accuracy ✔️

Bayesian Additive Regression Trees

Why BART for multiple treatments?

• Coherent posterior intervals ❓
• Heterogenous treatment effects ❓
• Accessibility ❓
• Accuracy ❓

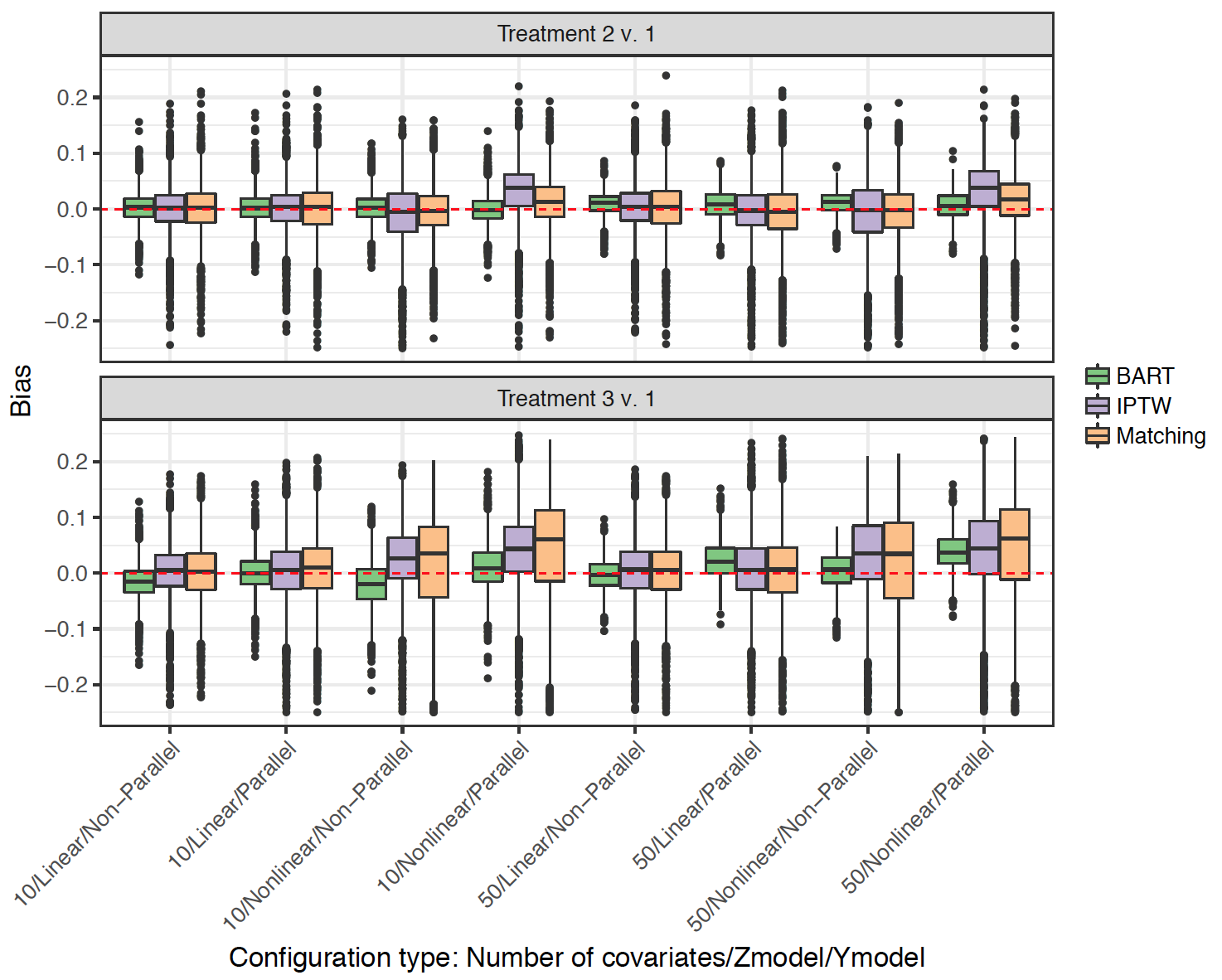
Simulation study

6 factorial design using dbarts package in R

• Ratio of $n_1$ : $n_2$ : $n_3$
• $n$
• No. of predictors
• $P(A|X)$
• Predictor strength alignment
• Response surfaces (parallel?)

3 lung cancer treatments

ATT’s: generalizable to population receiving robotic treatment

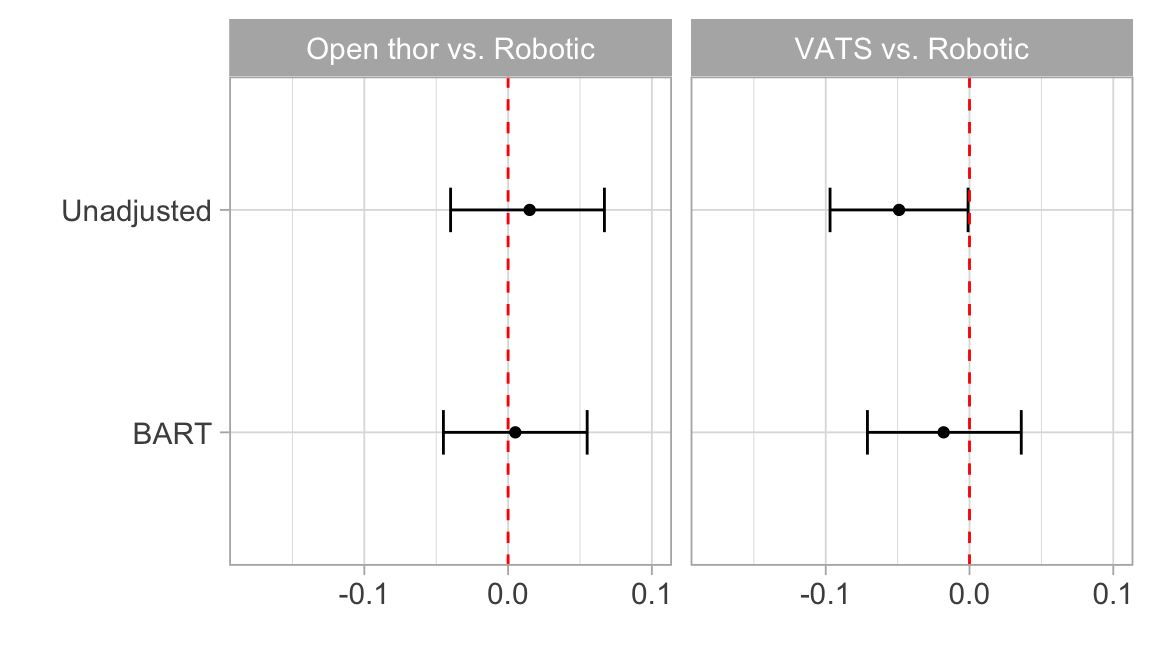
Comments

• Attentuation of effect comparing VATS vs. Robotic
  • distinct cohorts

• BART shows promise for causal inference with multiple treatments
  • expanded simulations required
  • formal paper ready sometime soon?

Comments

Github site: https://github.com/statsbylopez/ci-bart

Twitter: @statsbylopez